Learning to Optimize Join Queries With Deep Reinforcement Learning
Background
传统的多表 join 算法采用的是动态规划:
- 从初始 query graph 开始
- 找到 cost 最少的 join
- 更新 query graph 直到只剩下一个节点。但这种贪心策略并不会保证一定会选到合适的 join order,因为它只直观表示了每个 join 的
短期cost。例如:
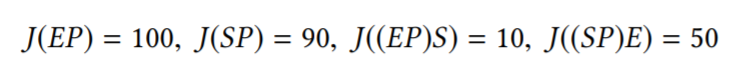
动态规划的结果 cost 为 140,而最优解的 cost 为 110。
Learning to Optimize Join Queries With Deep Reinforcement Learning 论文中将 join 问题表示为马尔可夫决策过程(MDP),然后构建了一个使用深度 Q 网络(DQN)的优化器,用来有效地优化 join 顺序。
Method
将连接排序表示为 MDP:
- 状态G:a query graph
- 动作c:a join
- 下一个状态G’:join后的query graph
- 奖励J(c):join的估算成本
用 Q-Learning 算法来解决 join 顺序 MDP。在 Q-Learning 中最关键的是得到 Q 函数 Q(G,c),它可以知道当前 query graph 中进行每个 join 的长期cost。如果我们可以访问真正的 Q(G,c),就可以对传统的动态规划进行改进:
- 从初始 query graph 开始
- 找到 Q(G,c) 值最小的 join
- 更新 query graph 直到只剩下一个节点,从而得到最优的 join order。实际上我们无法访问真正的 Q 函数,因此,我们需要训练一个神经网络,它接收 (G,c) 作为输入,并输出估算的 Q(G,c)。在论文中算法如下,给定query:

状态 G 和动作 c 的特征化
- query graph 中的每个关系的所有属性放入集合 A-G 中;join 左侧的所有属性放入集合 A-L 中;join 右侧的所有属性放入集合 A-R 中。并使用 1-hot 向量来编码。对于该例子,论文中表示如下:

- 对于查询中的每个选择,我们可以获得 selectivity ∈ [0,1](用来估计选择后存在的元组占选择前总元组的比例),我们需要根据 selectivity 的值去更新向量。例如:

- 还可以根据在物理计划中选择的具体 join 算法去产生新的 1-hot 向量(例如,IndexJoin 为 [1 0], HashJoin 为 [0 1]),与原向量进行串联,如下:

根据在论文 2.5 节的假设:
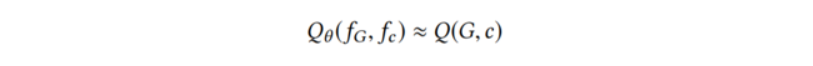
在这里我们就可以知道 query graph 特征 fG 为 fG = AG,join 决策特征 fc 为 fc = A-L ⊕ A-R,对于一个特定的元组(G,c)特征化为 fG ⊕ fc。
模型训练
DQ 使用多层感知机(MLP)神经网络来表示 Q 函数。它以(G,c)的最终特征化 fG ⊕ fc 作为输入。在实验中发现,两层的 MLP 可以提供最佳表现。模型使用随机梯度下降算法进行训练。
执行
训练后,在原有基础上再对多表 join 算法进行改进:
- 从初始 query graph 开始
- 使每个 join 特征化
- 找到模型估计的 Q 值最小的 join(即神经网络的输出)
- 更新 query graph 直到只剩下一个节点,从而得到最优的 join order。在执行过程中,还可以对 DQ 进行进一步微调。
Experiment Result
论文中使用了 Join Order Benchmark(JOB) 来评估 DQ。这个数据库由来自 IMDB 的 21 个表组成,并提供了 33 个查询模板和 113 个查询。查询中的连接关系大小范围为 5 到 15 个。当连接关系的数量不超过 10 个时,DQ 从穷举中收集训练数据。
将 DQ 与几个启发式优化器(QuickPick 和 KBZ)以及经典动态规划(left-deep、right-deep、zig-zag)进行比较。对每个优化器生成的计划进行评分,并与最优计划(通过穷举获得)进行比较。
此外,论文中设计了 3 个成本模型:
- Cost Model 1(Index Mostly):模拟内存数据库并鼓励使用索引连接
- Cost Model 2(Hybrid Hash):仅考虑具有内存预算的散列连接和嵌套循环连接
- Cost Model 3(Hash Reuse):考虑重用已构建的散列表
进行了 4 轮交叉验证后,确保仅对未出现在训练工作负载中的查询进行 DQ 评估(对于每种情况,论文中在 80 个查询上训练并测试其中的 33 个)。计算查询的平均次优性,即“成本(算法计划)/ 成本(最佳计划)”,这个数字越低越好。例如,对 Const Model 1,DQ 平均距离最佳计划 1.32 倍。结果如下:
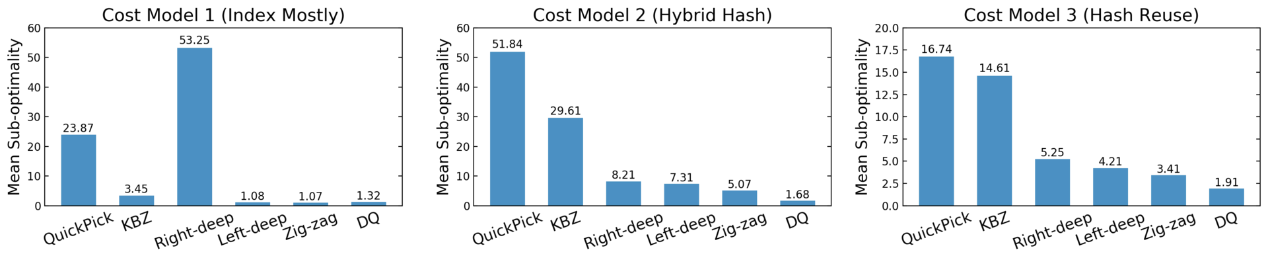
在所有成本模型中,DQ 在没有指数结构的先验知识的前提下可以与最优解决方案一比高下。对于固定的动态规划,情况并非如此:例如,left-deep 在 CM1 中产生了良好的计划,但在 CM2 和 CM3 中效果没有那么好。同样,right-deep在 CM1 中没有竞争力,但如果使用 CM2 或 CM3,right-deep 不是最差的。需要注意的是,基于学习的优化器比手动设计的算法更强大,可以适应工作负载、数据或成本模型的变化。
此外,DQ 以比传统动态规划快得多的速度产生了良好的计划:
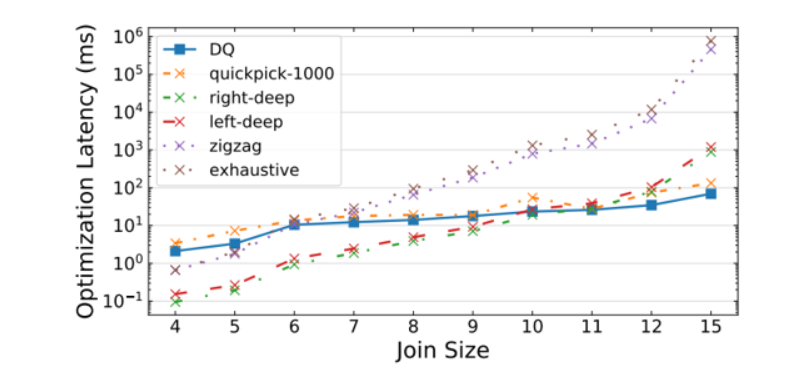
对于最大的连接(15),DQ 的速度是穷举的 10000 倍,比 zig-zag 快 1000 倍,比 left-deep 和 right-deep 快 10 倍。
Future work
本文研究中存在的不足:
- 奖励值(即J(c))依赖于数据库系统的代价模型,当代价估计错误时,算法的 join 计划无法达到最优
- 需要大量的 query 进行训练,估计的 Q 函数的值才能趋向稳定
可以拓展的思路:
同样使用强化学习,参考于 SkinnerDB: Regret-Bounded Query Evaluation via Reinforcement Learning,一条 join query 的执行框架如下:
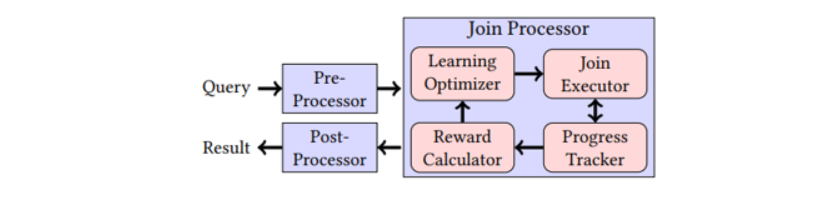
查询时,Pre-Processor 首先通过一元谓词过滤基表,接着由 Join Processor 生成查询的连接顺序与执行结果,最后调用 Post-Processor 对结果进行分组、聚合与排序等操作。
Join Processor 包括 4 部分,Join Processor 将每个连接操作分为多个时间片,每个时间片首先由 Learning Optimizer 选择连接顺序,选中的连接顺序由特定的 Join Executor 执行,每次执行固定时长,并将执行结果加入结果集中。Progress Tracker 跟踪被处理的数据,最后由 Reward Calcultor 计算连接顺序的得分。当所有数据被连接后,完成连接操作。学习优化器使用强化学习领域的上限置信区间算法(UCT),在每个时间片中根据连接顺序的枚举空间生成搜索树,并选择一条路径。UCT 算法的特点即不依赖任何具体示例的参数设置,能够适用于较大的搜索空间。
该算法不需要任何查询上下文及 Cardinality 估计模型。