背景

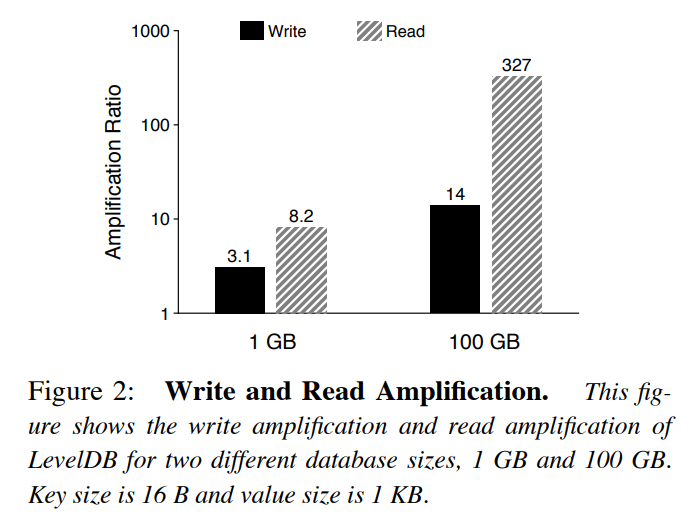
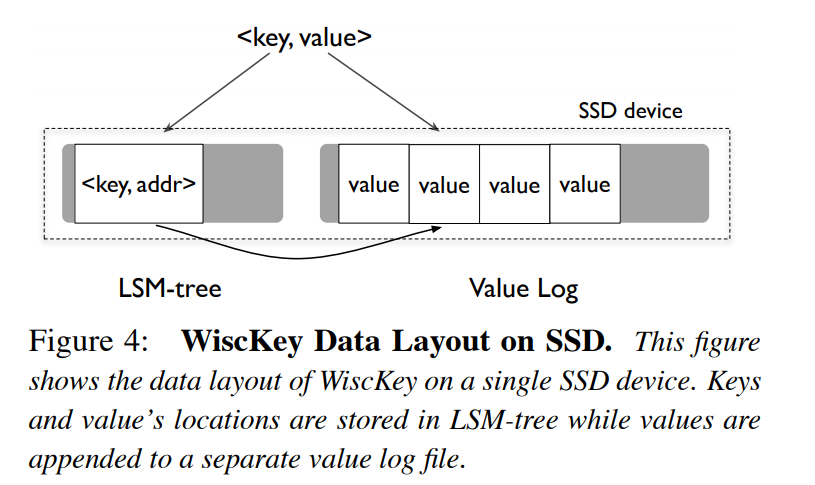
Bourbon 基于 WiscKey（比 LevelDB 和 RocksDB 更快的 LSM-Tree 存储系统）实现。本文通过对 WiscKey 的实验分析，总结了五条指南。Bourbon 应用了这些指南，将 WiscKey 与学习索引相结合，利用学习索引实现快速查找。

设计与实现

Five learning guidelines

1. Favor learning files at lower levels (生命周期更长)
2. Wait before learning a file (连续的 compaction 会在每一层生成生命周期非常短的新文件)
3. Do not neglect files at higher levels (可以提供多种内部查询方式)
4. Be workload- and data-aware (在不同的场景中查找会有很大差异)
5. Do not learn levels for write-heavy workloads (变化很快)

Beneficial regimes

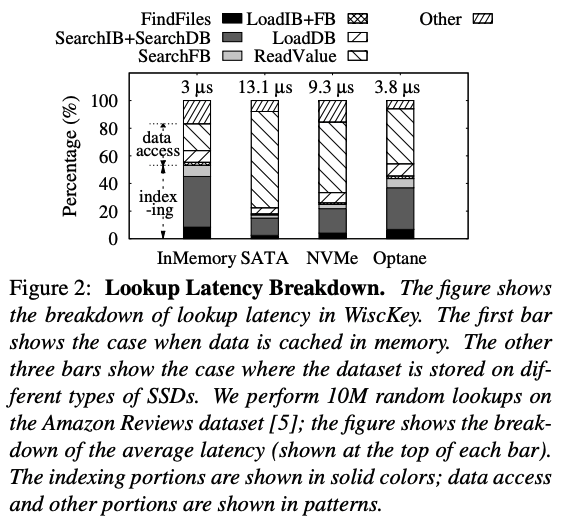
学习索引只能缩短检索时间。

Bourbon Learning

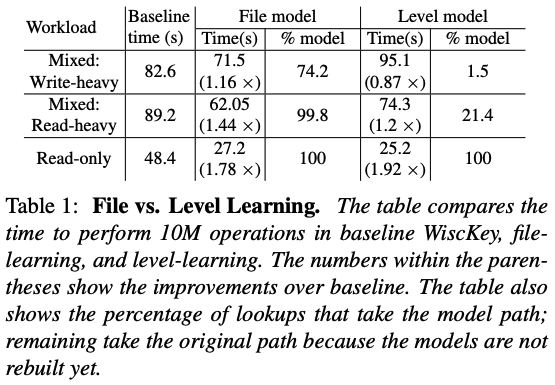
Bourbon 使用分段线性回归（PLR）对数据进行建模，PLR 在学习和查找过程中开销较低，而且空间开销也很小。Bourbon 可以学习单个 SSTables文件（File Learning）或整个层级（Level Learning）。层级学习对于只读工作负载收益更高，而对于混合工作负载，层级学习的性能不如文件学习。

为了训练 PLR 模型，Bourbon 使用了 Greedy-PLR 算法，一次处理一个数据点，如果数据点不能在不超出定义的误差限制的情况下被添加到当前的线段中，那么将创建一个新的线段，并将数据点添加到其中，最终 Greedy-PLR 生成了一组代表数据的线段。Greedy-PLR 的运行时间与数据点的数量呈线性关系。

Cost-benefit analyzer (CBA)

成本效益分析（Cost-Benefit Analyzer, CBA）的目的是过滤掉不值得学习的生命周期较短的文件。CBA 在同一层级使用之前文件的统计信息。

为了过滤短生命周期文件，Bourbon 在学习文件之前会等待一个时间阈值 $T_{wait}$。对一个文件进行学习的最大耗时约为 40 毫秒，因此 Bourbon 将 $T_{wait}$ 设置为 50 毫秒。但是，学习一个长期存在的文件也可能没有好处。作者实验发现更低层级的文件通常寿命更长，对于有的工作负载和数据集，他们服务的查询操作比更高层级的文件要少得多。因此，除了考虑模型对应的开销以外，还需要考虑模型可能带来的收益。如果一个模型的收益（$B_{model}$）大于构建该模型的开销（$C_{model}$），那么该模型就是有利的。

Estimating the cost ($C_{model}$)

如果假定学习过程发生在后台（有很多空闲的 core），那么 $C_{model}$ 开销就为 0。不过 Bourbon 采取了保守的做法，假设学习线程会对系统产生干扰，导致性能变慢。因此，论文将 $C_{model}$ 开销定义为与 $T_{build}$ 相等，即文件训练 PLR 模型的时间。由于 $T_{build}$ 与文件中数据点的数量成线性比例，我们将 $T_{build}$ 定义为文件中数据点的数量与训练一个数据点的平均时间的乘积。

Estimating the benefit ($B_{model}$)

Bourbon 定义模型带来的收益如下:

$$
B_{model} = (T_b - T_m) * N
$$

• $T_{b}$: 在基线中查找的平均时间
• $T_{m}$: 在模型路径中查找的平均时间
• $N$: 文件在其生命周期内的查找次数

然后又将查询操作又划分成了 negative 和 positive，因为大多数 negative 的查询操作在 filter 处就终止了，所以最终的收益模型为:

$$
B_{model} = ((T_{n.b} - T_{n.m}) * N_n) + ((T_{p.b} - T_{p.m}) * N_p)
$$

• $N_{n}$ & $N_{p}$: negative 和 positive 的查询数量
• $T_{n.b}$ & $T_{p.b}$: 在基线中 negative 和 positive 查找的平均时间
• $T_{n.m}$ & $T_{p.m}$: 在模型路径中 negative 和 positive 查找的平均时间

为了估计查找次数（$N_{n}$ & $N_{p}$）和查找所需时间（$T_{n.b}$ & $T_{p.b}$），CBA 维护了这些文件在其生命周期内和在同一层级上的文件的统计信息（因为统计信息在不同层级之间存在显著差异）。

这些估算在 $T_{wait}$ 期间完成:

• $T_{n.b}$ & $T_{p.b}$: 在 $T_{wait}$ 期间，查询将通过基线路径，这些查询时间用于估计 $T_{n.b}$ 和 $T_{p.b}$
• $T_{n.m}$ & $T_{p.m}$: 通过同一层级所有其他文件的平均值进行估计
• $N_{n}$ & $N_{p}$: CBA 首先获取该层级中其他文件的平均 negative 查找和 positive 查找，然后，将其按 $f = s / s’$ 的倍数进行缩放，其中 $s$ 是文件的大小，$s’$ 是该层级的文件的平均大小

如果 $C_{model} < B_{model}$，文件将会开始训练。如果多个文件同时开始训练，则将它们放在一个最大优先级队列中，从而使收益最大的文件能够先被训练。

未来可能的改进方向包括：

1. 对 $N_{n}$, $N_{p}$, $T_{n.m}$, $T_{p.m}$ 进行更精确的估计
2. 改进计算 $C_{model}$ 开销的方法，使其不仅仅是 $T_{build}$
3. 使用另外的函数对训练队列进行排序，而非 $B_{model} - C_{model}$

Bourbon: Putting it All Together

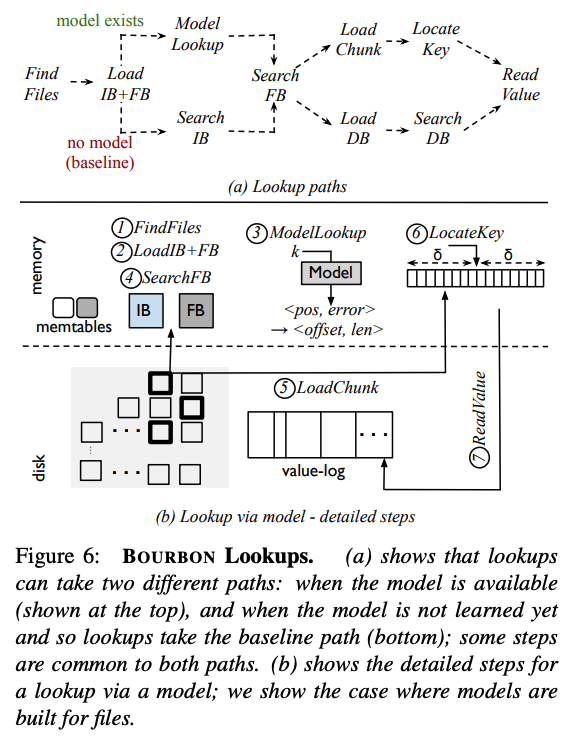
评估

参考

1. From WiscKey to Bourbon: A Learned Index for Log-Structured Merge Trees
2. Presentation video at OSDI ‘20
3. Presentation slides at OSDI ‘20

背景

读写放大

LSM-Tree key-value 存储存在读写放大的问题，例如对于LevelDB来说：

• 写放大：假如每一层的大小是上一层的 10 倍，那么当把 i-1 层中的一个文件合并到 i 层中时，LevelDB 需要读取 i 层中的文件的数量多达 10 个，排序后再将他们写回到 i 层中去。所以这个时候的写放大是 10。对于一个很大的数据集，生成一个新的 SSTable 文件可能会导致 L0-L6 中相邻层之间发生合并操作，这个时候的写放大就是50（L1-L6中每一层是10）。

• 读放大：(1) 查找一个 key-value 对时，LevelDB 可能需要在多个层中去查找。在最坏的情况下，LevelDB 在 L0 中需要查找 8 个文件，在 L1-L6 每层中需要查找 1 个文件，累计就需要查找 14 个文件。(2) 在一个 SSTable 文件中查找一个 key-value 对时，LevelDB 需要读取该文件的多个元数据块。所以实际读取的数据量应该是：index block + bloom-filter blocks + data block。例如，当查找 1KB 的 key-value 对时，LevelDB 需要读取 16KB 的 index block，4KB的 bloom-filter block 和 4KB 的 data block，总共要读取 24 KB 的数据。在最差的情况下需要读取 14 个 SSTable 文件，所以这个时候的写放大就是 24*14=336。较小的 key-value 对会带来更高的读放大。

WiscKey 论文中针对 LevelDB 测试的读写放大数据：

存储硬件

在 SSD 上，顺序和随机读写性能差异不大。对于写操作而言，由于随机写会对 SSD 的寿命造成影响，顺序写的特性应该保留，对于读操作来说，顺序读和随机读的性能测试如下图所示：

每次请求数据的 size 越大，SSD 的随机读与顺序读差距越小，并发数越大，SSD 的随机读与顺序读差距也越小。

WiscKey

WiscKey 包括四个关键思想：

(1) KV 分离，只有 key 在 LSM-Tree 上。
(2) 在 KV 分离后，value 采用顺序追加写，不保序。因此范围查询中，WiscKey 使用并行 SSD 设备的随机读特性查询 value。
(3) 使用 crash-consistency 和 garbage-collection 有效管理 value log。
(4) 通过删除 LSM-Tree 日志而不牺牲一致性来优化性能。

KV 分离

KV 分离的设计要点如下：

• key 存在 LSM-Tree 上。
• value 存在单独的 value log 中。
• 插入/更新数据的时候，首先将 value 追加到value log，然后将 key 插入 LSM-Tree 中。
• 删除数据的时候，只是将 key 在 LSM-Tree 中删除，value log 的数据不需要改变，因为 WiscKey 会有垃圾回收机制处理对应的 value。
• 读取数据时，先读 LSM-Tree，然后读 value log。

KV 分离对应的 Challenges

Parallel Range Query

1. 范围查询时，WiscKey 从 LSM-Tree 中读取多个 key 的元数据信息 <key, address>。
2. 将这些 <key, address> 放入队列。
3. 预读线程（默认32个）会从队列中获取 value 的地址，然后并行读取 value 数据。

Garbage Collection

Value log 结构如图所示，其由 value_entry 组成，每个value_entry 是一个四元组 (key size, value size, key, value)。另外，Value log 有两个指针 head 和 tail，tail 指向 Value log 的起点；head 指向文件的尾部，所有新的数据都将追加到 head 位置。

垃圾回收时，线程将从 tail 指向的位置开始，每次读取一个 chunk 的数据（比如几MB），对于 chunk 中的每一个 value_entry，在 LSM-Tree 中查找 key 以便判断该 value_entry 是否仍然有效。如果有效，则将该条目追加到 head 指针指向的位置，并且需要更新 LSM-Tree 的记录，因为 value 的地址已经变了；如果无效，则将其舍弃。

同时，为了避免出现数据不一致（如在垃圾回收过程中发生了 crash），需要保证在释放对应的存储空间之前追加写入的新的有效 value 和新的 tail 指针持久化到了设备上。具体的步骤如下：

• 垃圾回收在将 value 追加到 vLog 之后，在 vLog 上调用 fsync()
• 同步地将新的 value 地址和 tail 指针地址写入到 LSM-Tree 中。（tail 指针的存储形式为 <‘‘tail’’, tail-vLog-offset>）
• 最后回收 vLog 旧的数据空间

Crash Consistency

1. 如果不能在 LSM-Tree 中查询到对应的 key，那么处理方式和传统的 LSM-Tree 一样，返回空或者 key 不存在，即便其 value 已经写入到了 vLog 文件中，也会对其进行垃圾回收。
2. 如果 LSM-Tree 中存在要查询的 Key，则会进行校验。校验首先校验从 LSM-Tree 中查询到的 value 地址信息是否在有效的 vLog 文件范围内；其次校验该地址对应的 value 上存取的 key 和要查询的 key 是否一致。如果校验失败，则删除 LSM-Tree 中相应 key，并返回 key 不存在。
3. 另外，还可以引入 magic number 或 checksum 来校验 key 和 value 是否匹配。

总结

WiscKey 基于 LevelDB，设计了一个针对 SSD 进行优化的持久化 KV 存储方案，它的核心思想就是将 key 和 value 分离，key 存储在 LSM-Tree 中，value 存储在 value log 中，保留了 LSM-Tree 的优势，减少读写放大，发挥了 SSD 顺序写与并行随机读性能好的优势，但在小 value 场景以及大数据集范围查询下，WiscKey 的性能比 LevelDB 差。

参考

1. Lu L, Pillai T S, Arpaci-Dusseau A C, et al. WiscKey: separating keys from values in SSD-conscious storage[C] 14th USENIX Conference on File and Storage Technologies (FAST 16). 2016: 133-148.
2. LevelDB 源码分析（一）：简介
3. WiscKey: Separating Keys from Values in SSD-conscious Storage