概述

ALEX 是一个可更新的内存型学习索引。对比 B+Tree 和 Learned Index，ALEX 的目标是：(1)插入时间与 B+Tree 接近，(2)查找时间应该比 B+Tree 和 Learned Index 快，(3)索引存储空间应该比 B+Tree 和 Learned Index 小，(4)数据存储空间（叶子节点）应该与 B+Tree 相当。

ALEX 的设计如下：

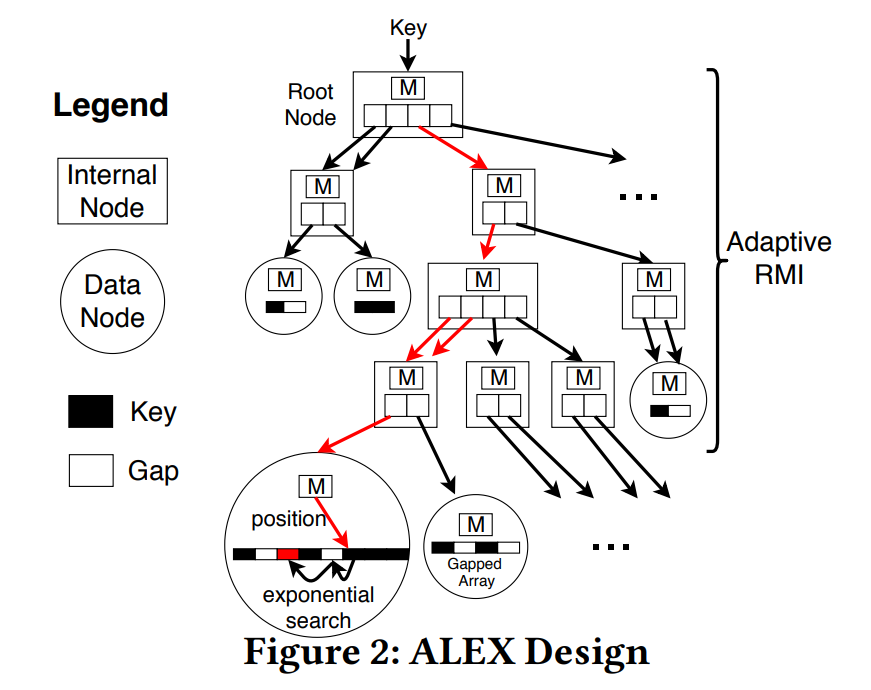
• ALEX 动态调整 RMI 的形状和高度，节点可以进行扩展和分割
• ALEX 使用 Exponential Search 来寻找叶子层的 key，以纠正 RMI 的错误预测，这比 Binary Search 效果更好
• ALEX 在数据节点上使用 Gapped Array(GA)，将数据插入在自己预测的地方。这和 RMI 有很大的不同。RMI 是先排好序，让后训练模型去拟合数据。而 ALEX 是在模型拟合完数据后，将数据在按照模型的预测值插入到对应的地方，这大大降低了预测的错误率
• ALEX 的 RMI 结构的目标不是产生同等大小的数据节点，而是产生 key 分布大致为线性的数据节点，以便线性模型能够准确地拟合。因此，ALEX 中的内部节点更加灵活。例如下图中节点 A 中 keys 的范围在 [0,1) 内，并有四个指针。ALEX 将 keys 范围 [0,1/4) 和 [1/2,1) 分配给数据节点（因为这些空间的 CDF 是线性的），并将 [1/4,1/2) 分配给另一个内部节点（因为CDF是非线性的，RMI需要对这个空间进行更多的划分）。另外，多个指针可以指向同一个子节点，便于插入；限制每个内部节点的指针数量总是 2 的幂，便于节点可以在不重新训练的情况下分裂

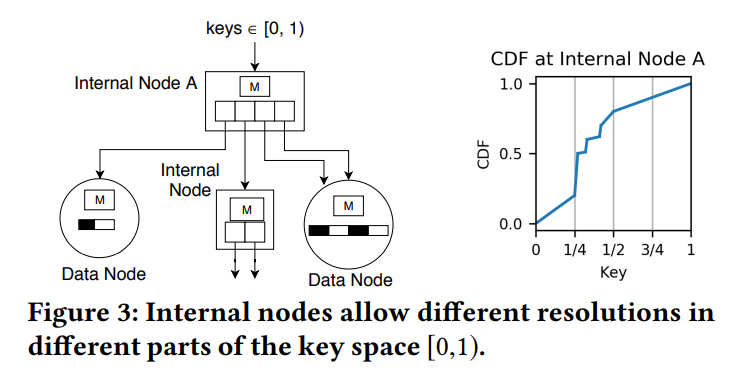
下面介绍 ALEX 的查询、插入、删除等步骤。

Lookups and Range Queries

查找时，从 RMI 的根节点开始，使用模型计算在哪一个位置，然后迭代地查询下一级的叶子节点，直到到达一个数据节点。在数据节点中使用模型来查询 key 在数组中的位置，如果预测失败，则进行 Exponential Search 以找到 key 的实际位置。如果找到了一个 key，读取对应值并返回记录，否则返回一个空记录。对于范围查询，首先找到第一个 key 的位置，该 key 不小于范围的起始值，然后扫描，直到到达范围的结束值，使用节点的 bitmap 跳过间隙，必要时跳到下一个数据节点。

Insert in non-full Data Node

插入逻辑与上述查找算法相同。在一个 non-full 的数据节点中，使用数据节点中的模型来预测插入位置。如果预测的位置不正确（不能保持有序），则做 Exponential Search 来找到正确的插入位置。如果插入位置为空，则直接插入，否则插入到最近的间隙中。Gapped Array实现了 O(logn) 插入时间。

Insert in full Data Node

Criteria for Node Fullness

ALEX 并不会让数据节点 100% 充满，因为在 Gapped Array 上的插入性能会随着间隙数量的减少而下降。需要在 Gapped Array 上引入了密度的下限和上限：dl, du ∈ (0, 1)，约束dl < du。密度被定义为被元素填充的位置的百分比。如果下一次插入使得密度超过了 du，那么这个节点就是满的。默认情况下，我们设置 dl=0.6，du=0.8。相比之下，B+Tree 的节点通常有 dl=0.5 和 du=1。

Node Expansion Mechanism

扩展一个包含 N 个 key 的数据节点，需要创建一个具有 N/dl 槽的新的较大的 Gapped Array。然后对线性回归模型进行缩放或重新训练，然后使用缩放或重新训练的模型对这个节点中的所有元素进行基于模型的插入。新的数据节点的密度处于下限 dl。下图为一个数据节点扩展的例子，数据节点内的 Gapped Array 从左边的两个槽扩展到右边的四个槽。

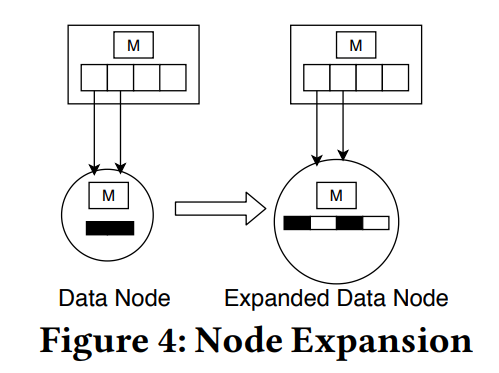
Node Split Mechanism

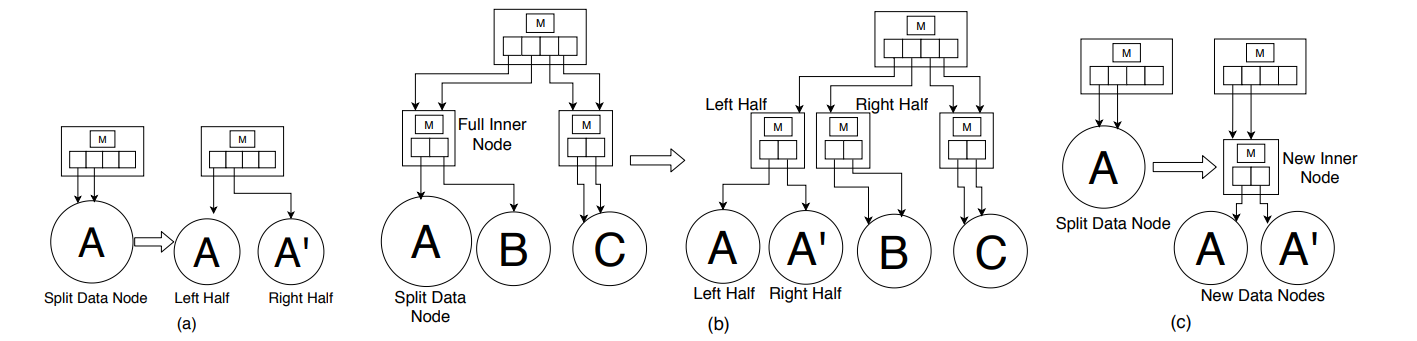
1. 水平分裂。有两种情况：(1) 如果待分裂的数据节点的父内部节点还没有达到最大的节点大小，父内部节点的指针数组可能有多余的指向待分裂数据节点的指针。如果有，则各让一半的指针指向两个新数据节点。否则，将父节点的指针数组的大小增加一倍，并为每个指针制作一个冗余的副本，来创建第二个指向分裂数据节点的指针，然后再分裂。下图(a)展示了一个不需要扩展父内部节点的侧向分裂的例子。(2) 如果父内部节点已经达到最大节点大小，那么我们可以选择拆分父内部节点，如下图(b)中所示。因为内部节点的大小为2的幂，所以总是可以拆分一个数据节点，不需要对拆分后的任何模型进行重新训练。分裂可以一直传播到根节点，就像在 B+Tree 中一样。
2. 向下分裂。如下图(c)所示，向下分裂将一个数据节点转换为具有两个子数据节点的内部节点。两个子数据节点中的模型是根据它们各自的 key 来训练的。

Delete and update

要删除一个 key，需要先找到该 key 的位置，然后删除它和它对应的值。删除不会移动任何现有的 key，所以删除是一个严格意义上的比插入更简单的操作，不会导致模型的准确性下降。如果一个数据节点由于删除而达到了密度下限 dl，那么就缩小数据节点（与扩大数据节点相反），以避免空间利用率过低。此外还可以使用节点内的成本模型来确定两个数据节点是否应该合并在一起，然而为了简单起见，ALEX 开源代码中并没有实现这些合并操作。
key 更新是通过结合插入和删除来实现的；值更新是通过查找 key 并将新值写入来实现的。

参考

1. ALEX: An Updatable Adaptive Learned Index

背景

Bourbon 基于 WiscKey（比 LevelDB 和 RocksDB 更快的 LSM-Tree 存储系统）实现。本文通过对 WiscKey 的实验分析，总结了五条指南。Bourbon 应用了这些指南，将 WiscKey 与学习索引相结合，利用学习索引实现快速查找。

设计与实现

Five learning guidelines

1. Favor learning files at lower levels (生命周期更长)
2. Wait before learning a file (连续的 compaction 会在每一层生成生命周期非常短的新文件)
3. Do not neglect files at higher levels (可以提供多种内部查询方式)
4. Be workload- and data-aware (在不同的场景中查找会有很大差异)
5. Do not learn levels for write-heavy workloads (变化很快)

Beneficial regimes

学习索引只能缩短检索时间。

Bourbon Learning

Bourbon 使用分段线性回归（PLR）对数据进行建模，PLR 在学习和查找过程中开销较低，而且空间开销也很小。Bourbon 可以学习单个 SSTables文件（File Learning）或整个层级（Level Learning）。层级学习对于只读工作负载收益更高，而对于混合工作负载，层级学习的性能不如文件学习。

为了训练 PLR 模型，Bourbon 使用了 Greedy-PLR 算法，一次处理一个数据点，如果数据点不能在不超出定义的误差限制的情况下被添加到当前的线段中，那么将创建一个新的线段，并将数据点添加到其中，最终 Greedy-PLR 生成了一组代表数据的线段。Greedy-PLR 的运行时间与数据点的数量呈线性关系。

Cost-benefit analyzer (CBA)

成本效益分析（Cost-Benefit Analyzer, CBA）的目的是过滤掉不值得学习的生命周期较短的文件。CBA 在同一层级使用之前文件的统计信息。

为了过滤短生命周期文件，Bourbon 在学习文件之前会等待一个时间阈值 $T_{wait}$。对一个文件进行学习的最大耗时约为 40 毫秒，因此 Bourbon 将 $T_{wait}$ 设置为 50 毫秒。但是，学习一个长期存在的文件也可能没有好处。作者实验发现更低层级的文件通常寿命更长，对于有的工作负载和数据集，他们服务的查询操作比更高层级的文件要少得多。因此，除了考虑模型对应的开销以外，还需要考虑模型可能带来的收益。如果一个模型的收益（$B_{model}$）大于构建该模型的开销（$C_{model}$），那么该模型就是有利的。

Estimating the cost ($C_{model}$)

如果假定学习过程发生在后台（有很多空闲的 core），那么 $C_{model}$ 开销就为 0。不过 Bourbon 采取了保守的做法，假设学习线程会对系统产生干扰，导致性能变慢。因此，论文将 $C_{model}$ 开销定义为与 $T_{build}$ 相等，即文件训练 PLR 模型的时间。由于 $T_{build}$ 与文件中数据点的数量成线性比例，我们将 $T_{build}$ 定义为文件中数据点的数量与训练一个数据点的平均时间的乘积。

Estimating the benefit ($B_{model}$)

Bourbon 定义模型带来的收益如下:

$$
B_{model} = (T_b - T_m) * N
$$

• $T_{b}$: 在基线中查找的平均时间
• $T_{m}$: 在模型路径中查找的平均时间
• $N$: 文件在其生命周期内的查找次数

然后又将查询操作又划分成了 negative 和 positive，因为大多数 negative 的查询操作在 filter 处就终止了，所以最终的收益模型为:

$$
B_{model} = ((T_{n.b} - T_{n.m}) * N_n) + ((T_{p.b} - T_{p.m}) * N_p)
$$

• $N_{n}$ & $N_{p}$: negative 和 positive 的查询数量
• $T_{n.b}$ & $T_{p.b}$: 在基线中 negative 和 positive 查找的平均时间
• $T_{n.m}$ & $T_{p.m}$: 在模型路径中 negative 和 positive 查找的平均时间

为了估计查找次数（$N_{n}$ & $N_{p}$）和查找所需时间（$T_{n.b}$ & $T_{p.b}$），CBA 维护了这些文件在其生命周期内和在同一层级上的文件的统计信息（因为统计信息在不同层级之间存在显著差异）。

这些估算在 $T_{wait}$ 期间完成:

• $T_{n.b}$ & $T_{p.b}$: 在 $T_{wait}$ 期间，查询将通过基线路径，这些查询时间用于估计 $T_{n.b}$ 和 $T_{p.b}$
• $T_{n.m}$ & $T_{p.m}$: 通过同一层级所有其他文件的平均值进行估计
• $N_{n}$ & $N_{p}$: CBA 首先获取该层级中其他文件的平均 negative 查找和 positive 查找，然后，将其按 $f = s / s’$ 的倍数进行缩放，其中 $s$ 是文件的大小，$s’$ 是该层级的文件的平均大小

如果 $C_{model} < B_{model}$，文件将会开始训练。如果多个文件同时开始训练，则将它们放在一个最大优先级队列中，从而使收益最大的文件能够先被训练。

未来可能的改进方向包括：

1. 对 $N_{n}$, $N_{p}$, $T_{n.m}$, $T_{p.m}$ 进行更精确的估计
2. 改进计算 $C_{model}$ 开销的方法，使其不仅仅是 $T_{build}$
3. 使用另外的函数对训练队列进行排序，而非 $B_{model} - C_{model}$

Bourbon: Putting it All Together

评估

参考

1. From WiscKey to Bourbon: A Learned Index for Log-Structured Merge Trees
2. Presentation video at OSDI ‘20
3. Presentation slides at OSDI ‘20